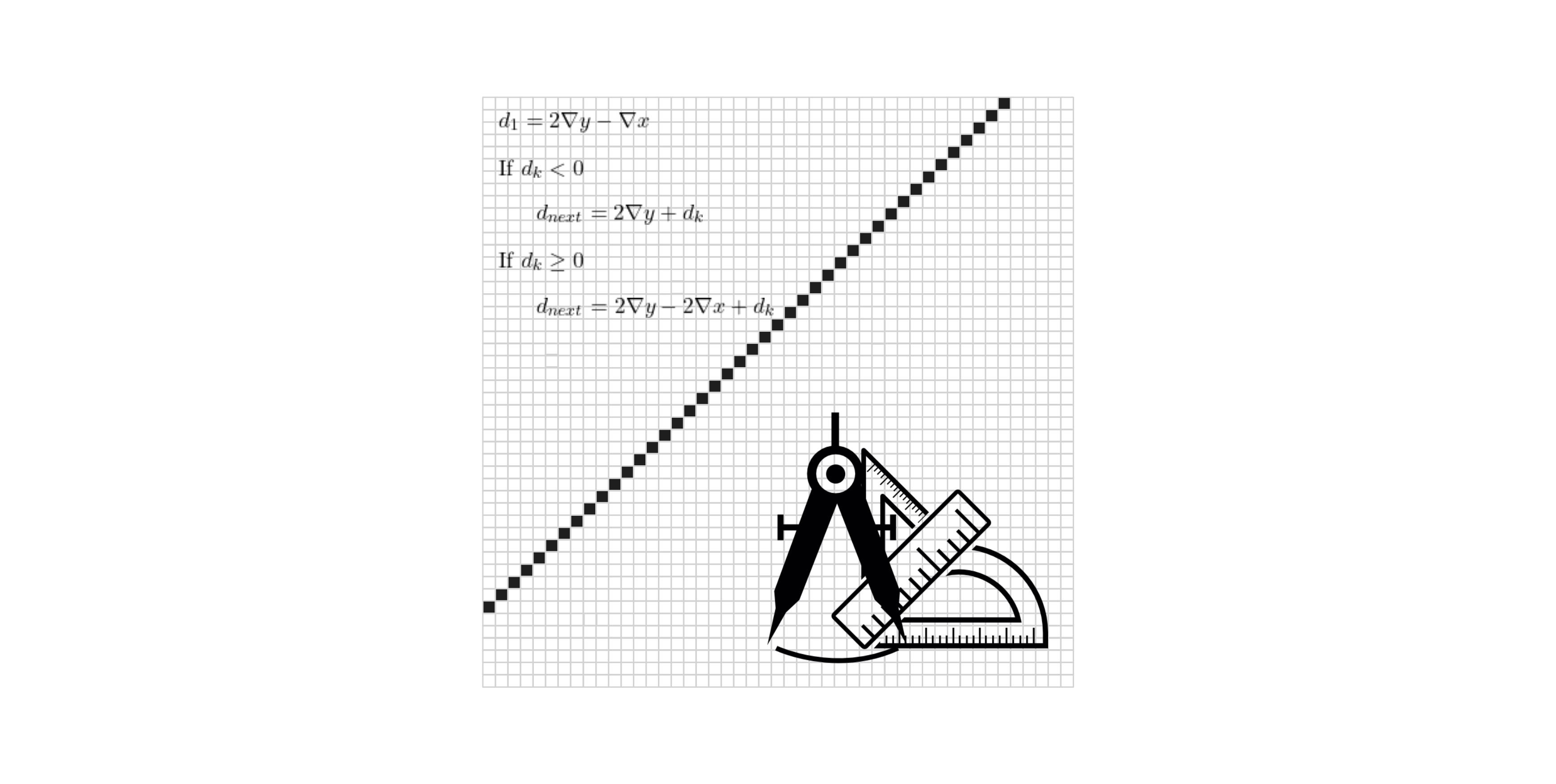
Xiaolin Wu’s Line Algorithm
This is an implementation of Xiaolin Wu’s Line Algorithm in Python. The algorithm is used to calculate a list of pixel coordinates with intensity values to form an anti-aliased line between two points on a 2D grid. It is widely used in computer graphics for rendering smooth lines on raster displays.
Overview
Xiaolin Wu’s Line Algorithm is an efficient method for drawing anti-aliased lines between two points on a pixel grid. Unlike traditional line-drawing algorithms like Bresenham’s, this algorithm assigns intensity values to pixels based on their proximity to the ideal line, resulting in smoother and visually appealing lines
Source code: https://github.com/byteblueprints/bresenham-algorithms
Description:
xiaolin_wu_line(x0, y0, x1, y1) generates a list of pixel coordinates along with their intensity values that form a smooth line between two points (x0, y0) and (x1, y1).
Parameters:
x0 (float): The x-coordinate of the starting point.y0 (float): The y-coordinate of the starting point.x1 (float): The x-coordinate of the ending point.y1 (float): The y-coordinate of the ending point.
Returns:
list of tuple: A list of tuples, where each tuple contains:x (int): The x-coordinate of the pixel.y (int): The y-coordinate of the pixel.i (float): The intensity value of the pixel (ranges from 0 to 1).
How it works:
- Anti-Aliasing: The algorithm calculates fractional intensities for pixels near the line to minimize the jagged appearance.
- Steep Lines: For lines with a steep slope, the roles of x and y are swapped to ensure proper handling.
- Endpoints: The algorithm handles endpoints separately for precision.
- Line Traversal: Pixels along the line are calculated using incremental updates based on the line’s slope.
Python Implementation:
import math
def xiaolin_wu_line(x0, y0, x1, y1):
"""
Generates a list of pixel coordinates and their intensity values that form a smooth line between two points (x0, y0) and (x1, y1)
using Xiaolin Wu's line algorithm.
Args:
x0 (float): The x-coordinate of the starting point.
y0 (float): The y-coordinate of the starting point.
x1 (float): The x-coordinate of the ending point.
y1 (float): The y-coordinate of the ending point.
Returns:
list of tuple: A list of tuples, each containing the coordinates (x, y) and intensity (i) of a pixel.
"""
def plot(x, y, c):
"""Helper function to return a pixel with its intensity."""
return (int(x), int(y), c)
def ipart(x):
"""Returns the integer part of x."""
return math.floor(x)
def round(x):
"""Rounds x to the nearest integer."""
return ipart(x + 0.5)
def fpart(x):
"""Returns the fractional part of x."""
return x - math.floor(x)
def rfpart(x):
"""Returns 1 minus the fractional part of x."""
return 1 - fpart(x)
pixels = []
steep = abs(y1 - y0) > abs(x1 - x0)
if steep:
x0, y0 = y0, x0
x1, y1 = y1, x1
if x0 > x1:
x0, x1 = x1, x0
y0, y1 = y1, y0
dx = x1 - x0
dy = y1 - y0
gradient = dy / dx if dx != 0 else 1
# Handle the first endpoint
xend = round(x0)
yend = y0 + gradient * (xend - x0)
xgap = rfpart(x0 + 0.5)
xpxl1 = xend # This will be used as the first pixel
ypxl1 = ipart(yend)
if steep:
pixels.append(plot(ypxl1, xpxl1, rfpart(yend) * xgap))
pixels.append(plot(ypxl1 + 1, xpxl1, fpart(yend) * xgap))
else:
pixels.append(plot(xpxl1, ypxl1, rfpart(yend) * xgap))
pixels.append(plot(xpxl1, ypxl1 + 1, fpart(yend) * xgap))
intery = yend + gradient # First y-intersection for the main loop
# Handle the second endpoint
xend = round(x1)
yend = y1 + gradient * (xend - x1)
xgap = fpart(x1 + 0.5)
xpxl2 = xend # This will be used as the last pixel
ypxl2 = ipart(yend)
if steep:
pixels.append(plot(ypxl2, xpxl2, rfpart(yend) * xgap))
pixels.append(plot(ypxl2 + 1, xpxl2, fpart(yend) * xgap))
else:
pixels.append(plot(xpxl2, ypxl2, rfpart(yend) * xgap))
pixels.append(plot(xpxl2, ypxl2 + 1, fpart(yend) * xgap))
# Main loop
for x in range(xpxl1 + 1, xpxl2):
if steep:
pixels.append(plot(ipart(intery), x, rfpart(intery)))
pixels.append(plot(ipart(intery) + 1, x, fpart(intery)))
else:
pixels.append(plot(x, ipart(intery), rfpart(intery)))
pixels.append(plot(x, ipart(intery) + 1, fpart(intery)))
intery += gradient
return pixels