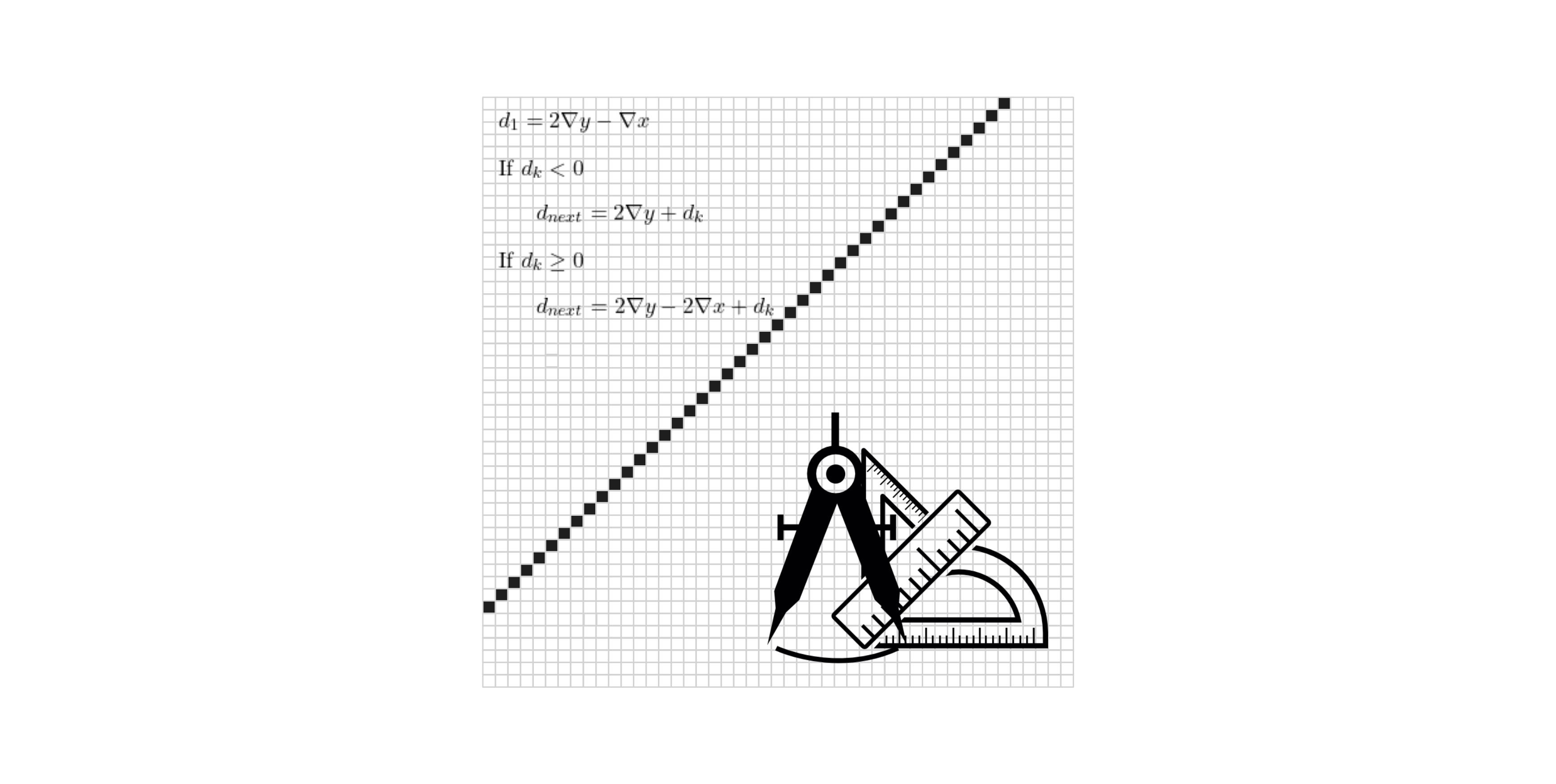
Overview
Bresenham’s Line Algorithm is an efficient method for drawing lines between two points on a pixel grid. This implementation handles horizontal, vertical, diagonal, and sloped lines with any given start and end points.
Source code: https://github.com/byteblueprints/bresenham-algorithms
Description:
get_bresenhams_line(x0, y0, x1, y1) generates a list of pixel coordinates that lie on a straight line between two points (x0, y0) and (x1, y1).
Parameters:
x0 (int): The x-coordinate of the starting point.y0 (int): The y-coordinate of the starting point.x1 (int): The x-coordinate of the ending point.y1 (int): The y-coordinate of the ending point.
Returns:
list of tuple: A list of pixel coordinates that lie on the line connecting(x0, y0)and(x1, y1).
How it works:
The algorithm determines the slope of the line between the start and end points and uses different strategies for different types of lines:
- Horizontal or Vertical Lines: If either the horizontal or vertical distance (
dxordy) is 0, it uses simple iteration along one axis. - Diagonal Lines: For lines with a slope of 1 (45-degree diagonal), the algorithm handles both x and y increments simultaneously.
- Other Slopes: For lines with slopes greater or less than 1, the algorithm adjusts based on the slope to minimize pixel calculations.
Python Implementation:
def get_bresenhams_line(x0, y0, x1, y1) -> list:
"""
Generates a list of pixel coordinates that form a line between two points (x0, y0) and (x1, y1) using Bresenham's line algorithm.
Args:
x0 (int): The x-coordinate of the starting point.
y0 (int): The y-coordinate of the starting point.
x1 (int): The x-coordinate of the ending point.
y1 (int): The y-coordinate of the ending point.
Returns:
list of tuple: A list of pixel coordinates that lie on the line connecting (x0, y0) and (x1, y1).
The function calculates the line using different cases based on the slope (m) and handles cases where the line is horizontal, vertical, or diagonal.
It uses Bresenham's algorithm to ensure efficient pixel plotting for all types of lines.
"""
dx = abs(x1 - x0)
dy = abs(y1 - y0)
# If the starting and ending points are the same, return the single point.
if dx == 0 and dy == 0:
return [(x0, y0)]
step_x = 1 if x0 < x1 else -1
step_y = 1 if y0 < y1 else -1
current_x = x0
current_y = y0
d = 2 * dy - dx
pixels_to_be_colored = [(x0, y0)]
# Handle horizontal or vertical lines (when either dx or dy is 0)
if dy == 0 or dx == 0:
while True:
if y0 != y1:
current_y = current_y + step_y
else:
current_x = current_x + step_x
pixels_to_be_colored.append((current_x, current_y))
if current_x >= x1 and current_y >= y1:
break
else:
m = dy / dx
# Handle lines with slope equal to 1 (45 degree diagonal)
if m == 1:
while True:
current_y = current_y + step_y
current_x = current_x + step_x
pixels_to_be_colored.append((current_x, current_y))
if current_x >= x1 and current_y >= y1:
break
# Handle lines with slope less than 1
elif m < 1:
while True:
current_x = current_x + 1
if d >= 0:
current_y = current_y + step_y
d = d - 2 * dx
d = 2 * dy + d
pixels_to_be_colored.append((current_x, current_y))
if current_x >= x1 and current_y >= y1:
break
# Handle lines with slope greater than 1
elif m > 1:
while True:
current_y = current_y + 1
if d <= 0:
current_x = current_x + step_x
d = 2 * dy + d
d = d - 2 * dx
pixels_to_be_colored.append((current_x, current_y))
if current_x >= x1 and current_y >= y1:
break
return pixels_to_be_colored